To compare models we chose the Deviance Based R² presented by Berry, Hemming, Matov and Morris (2009).
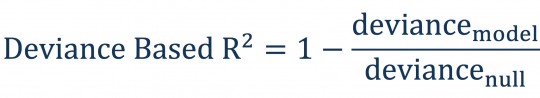
In a GLM framework the Deviance is analogous to the residual sum of squares in linear regression. A lower number implies a better fit.
Deviance Model is the deviance of the selected model and Deviance Null is the deviance of a model containing just a mean parameter.
The statistic can be loosely explained as the proportion of variation that is explained by the model, so a large value means that the model is performing well and a small value means that the model if performing badly.
Note that this statistic is calculated on the test dataset, so we don’t need to adjust for the number of parameters in the model when comparing between models.
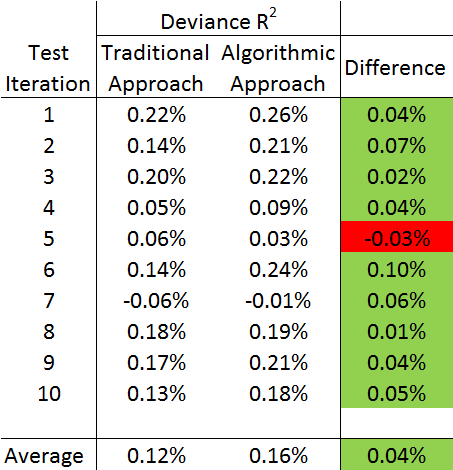
We can see that the algorithmic approach outperforms the traditional approach in 9/10 of the benchmark tests, with an average difference in Deviance Based R² of 0.04%. To understand whether this performance difference is a significant result we apply a one-sided paired t-test statistic. We are able to do this because each benchmark test is a paired result – both models were predicting the same set of holdout data. We calculate a t statistic of 2.275 which is significant at the 2.5% level of significance (p-value=0.024). Therefore we can say the Algorithmic Pricing approach performs significantly better than the Traditional approach.
